reduce the number of variables
- Thread starter Artur
- Start date
Removing a variable with a small variance is not a good idea. Anyway, after z-normalization (https://en.wikipedia.org/wiki/Standard_score#Standardizing_in_mathematical_statistics , which is always applied in TIMi modeler and nearly always applied in all other modeling algorithms), all the variables have a variance of 1. ...and a variable with a small initial variance might be an excellent predictor in a model.
A better choice would be to remove all the variables that have a too small (linear) correlation with the target. ...but then you can potentially make a wrong choice because there can still exist a very strong nonlinear relation with your target and you'll still remove the variable because its linear correlation is weak. A good example of such a variable is the "age" variable (in a commercial model): Here is an illustration (from the famous census-income dataset):
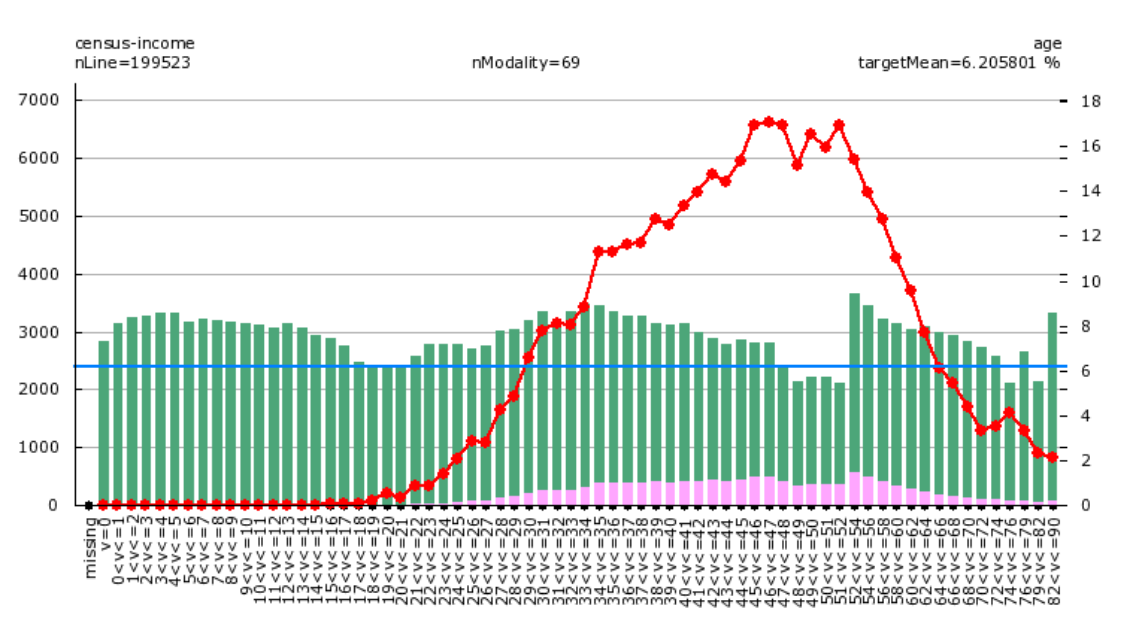
The age variable has a nonlinear pattern because we have:
* The older you are, the wealthier you are (for the ages below 60) (look at the red line above).
* The older you are, the poorer you are (for the ages above 60).
This "inversion of the trend" represents a nonlinear relationship.
This means that the linear correlation between the target and the variable "age" will be weak (and you will be tempted to "drop" the variable) although there exists a strong nonlinear relationship.
One of the best variables in the census-income dataset is the "dividends_from_stocks":
Let's have a look at this variable:
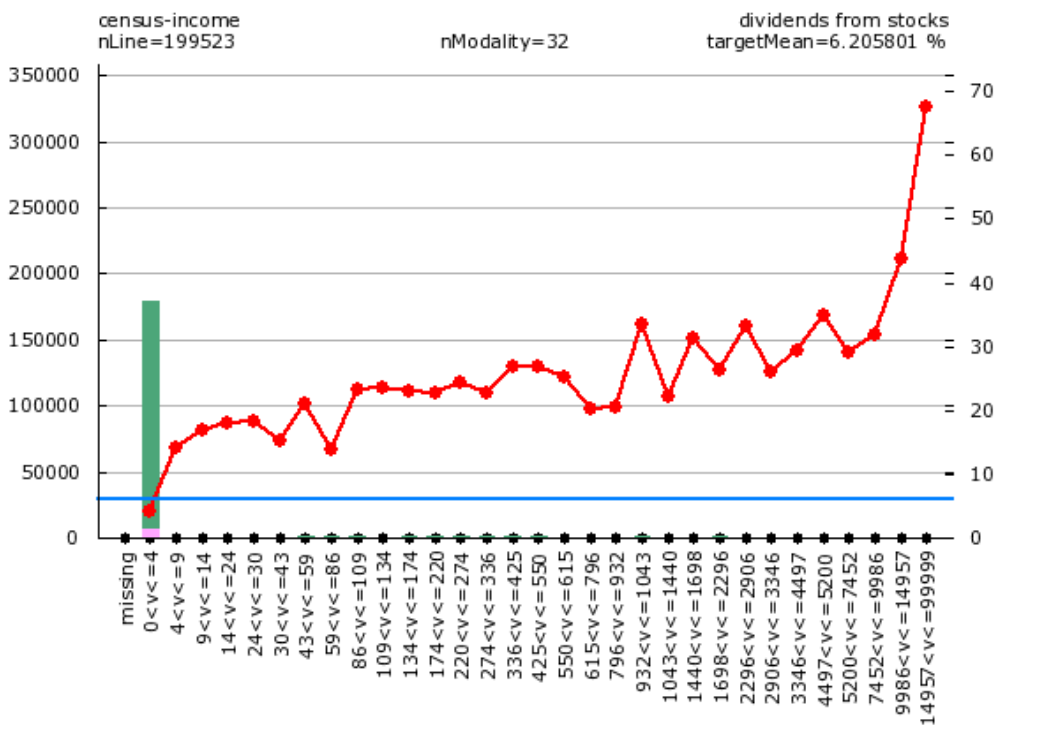
You can see that this variable has a very small variance because 99% of the values are "zero" (i.e. "0<v<=4" is actually "zero") (i.e. you should compare the eight of the green bar at 0 to the eight of the green bar at other values). This variable has also a very weak linear correlation with the target (because, 99% of the values are 0, so the *linear* correlation cannot be very high). BUT this is one of the best variables of the model!
Actually, a good solution would be to select the variables with the highest "univariate importance" (as computed inside the TIMi Audit reports): you'll have a much better variable selection. We attached a small Anatella graph that automatically extracts this "variable list" from the TIMi "audit report".
As explained above, selecting variables based on variance is not necessarily a good idea.
However, when you select variables based on:
* linear correlation,
* timi univariate importance
* or any other criteria...
... the question of the threshold still remains.
To reduce the number of variables, we have seen many people do the following 2 steps:
Step 1. keep only the variable with a "high" linear correlation with the target. This gives you a first set "A" of variable.
Step 2. Reduce the set "A" of variables by removing from this set the variables that are strongly correlated together. The idea is the following: "if two variables are correlated at 95%, then these 2 variables are virtually the same and you can safely remove one of the two".
Each of these two steps described here above requires you to define a threshold. So, let's analyze each step:
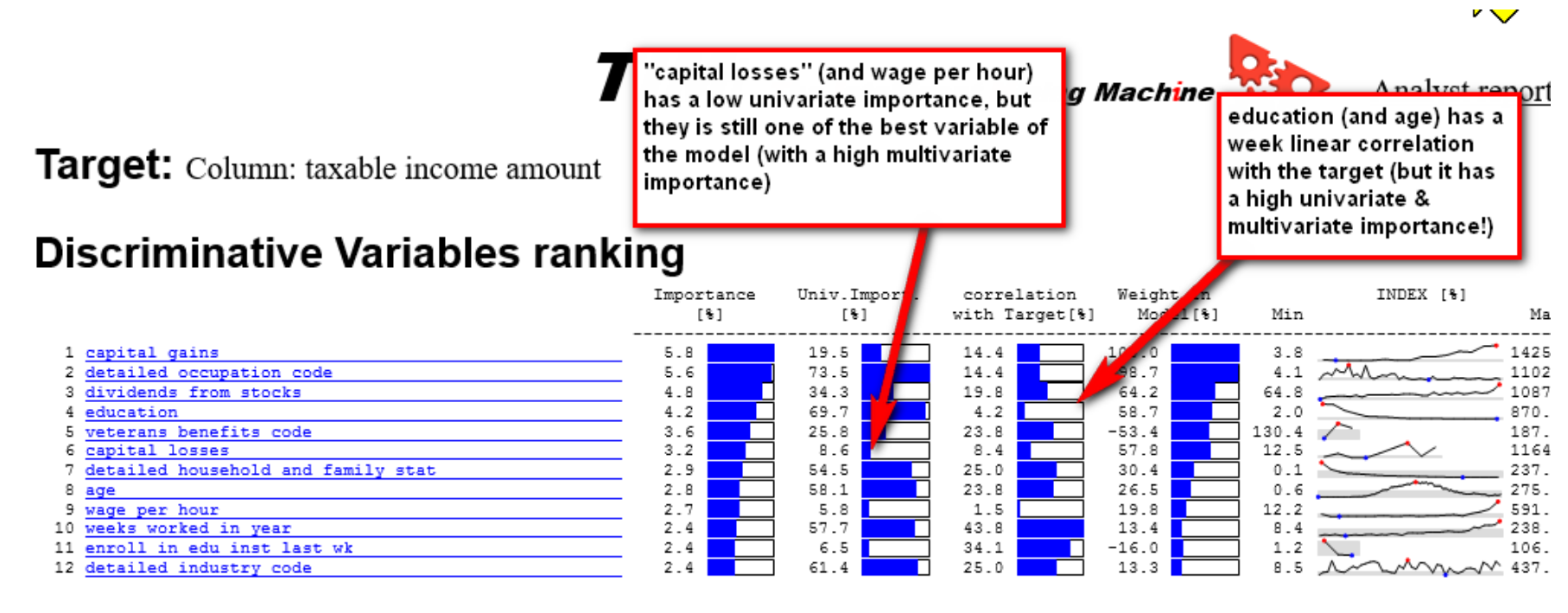
Step 1: As explained above, using the "linear correlation with the target" isn’t a good idea. You should rather use the "timi univariate importance". You could use a threshold of 5% on "timi univariate importance". You might be tempted to think the following: "A threshold of 5% on the "timi univariate importance" means that, in the worst case, you'll lose 5% of AUC inside your final model". This sentence is not true because there can exist inside you dataset some "multivariate effects" that suddenly transform a "bad" variable (with a low "timi univariate importance") to an excellent variable (with a high "multivariate importance" in the top 10 variables). This is more common than you might think (although, with a threshold of 5%, you should be safe): For example: look at the variable "capital losses" (always in the census-income dataset):
Step 2: Two variables A and B that are correlated at 95% are very similar but there still exists 5% difference between them. If your target size (i.e. the number of positive case inside a binary predictive model) is 1% (which is very common), then the 5% difference that exists between the two variables A and B might make an enormous difference: It can happen that a variable A is very good and a variable B is very bad (although they are correlated at 95%). So, for small target sizes, we would not remove any variable during step 2. If you have a large target size (i.e. the target size is 50% of the total dataset size), then you can remove either A or B (when A and B are correlated at 95%).
A better choice would be to remove all the variables that have a too small (linear) correlation with the target. ...but then you can potentially make a wrong choice because there can still exist a very strong nonlinear relation with your target and you'll still remove the variable because its linear correlation is weak. A good example of such a variable is the "age" variable (in a commercial model): Here is an illustration (from the famous census-income dataset):
The age variable has a nonlinear pattern because we have:
* The older you are, the wealthier you are (for the ages below 60) (look at the red line above).
* The older you are, the poorer you are (for the ages above 60).
This "inversion of the trend" represents a nonlinear relationship.
This means that the linear correlation between the target and the variable "age" will be weak (and you will be tempted to "drop" the variable) although there exists a strong nonlinear relationship.
One of the best variables in the census-income dataset is the "dividends_from_stocks":
Let's have a look at this variable:
You can see that this variable has a very small variance because 99% of the values are "zero" (i.e. "0<v<=4" is actually "zero") (i.e. you should compare the eight of the green bar at 0 to the eight of the green bar at other values). This variable has also a very weak linear correlation with the target (because, 99% of the values are 0, so the *linear* correlation cannot be very high). BUT this is one of the best variables of the model!
Actually, a good solution would be to select the variables with the highest "univariate importance" (as computed inside the TIMi Audit reports): you'll have a much better variable selection. We attached a small Anatella graph that automatically extracts this "variable list" from the TIMi "audit report".
As explained above, selecting variables based on variance is not necessarily a good idea.
However, when you select variables based on:
* linear correlation,
* timi univariate importance
* or any other criteria...
... the question of the threshold still remains.
To reduce the number of variables, we have seen many people do the following 2 steps:
Step 1. keep only the variable with a "high" linear correlation with the target. This gives you a first set "A" of variable.
Step 2. Reduce the set "A" of variables by removing from this set the variables that are strongly correlated together. The idea is the following: "if two variables are correlated at 95%, then these 2 variables are virtually the same and you can safely remove one of the two".
Each of these two steps described here above requires you to define a threshold. So, let's analyze each step:
Step 1: As explained above, using the "linear correlation with the target" isn’t a good idea. You should rather use the "timi univariate importance". You could use a threshold of 5% on "timi univariate importance". You might be tempted to think the following: "A threshold of 5% on the "timi univariate importance" means that, in the worst case, you'll lose 5% of AUC inside your final model". This sentence is not true because there can exist inside you dataset some "multivariate effects" that suddenly transform a "bad" variable (with a low "timi univariate importance") to an excellent variable (with a high "multivariate importance" in the top 10 variables). This is more common than you might think (although, with a threshold of 5%, you should be safe): For example: look at the variable "capital losses" (always in the census-income dataset):
Step 2: Two variables A and B that are correlated at 95% are very similar but there still exists 5% difference between them. If your target size (i.e. the number of positive case inside a binary predictive model) is 1% (which is very common), then the 5% difference that exists between the two variables A and B might make an enormous difference: It can happen that a variable A is very good and a variable B is very bad (although they are correlated at 95%). So, for small target sizes, we would not remove any variable during step 2. If you have a large target size (i.e. the target size is 50% of the total dataset size), then you can remove either A or B (when A and B are correlated at 95%).